并查集

并查集

两个不相干的集合之间的运算，用于解决图的一些问题，比如最小生成树，最短路径问题。

存储方法：

1	2	3	4	5
1	1	1	4	4

第一行表示每个节点，第二行表示每个节点所属的集合，用其中一个来代表（老大）。

1	2	3	4	5	6
1	1	3	3	4	4

这样也可以存储，第二行表示他的老大，可能出现次老大的情况，但都能说明他们同属于同一个集合。

只有下表为它本身的才是老大。一般用数组存放，第一行为数组下标。

一般问题的处理函数：

const int maxm = 1005;
int pre[maxm], r[maxm];

void init(int n)   //初始化
{
    for (int i = 0; i <= n; ++i)
    {
        pre[i] = i;
        r[i] = 0;
    }
}

int findpre(int x)  //找老大
{
    if (pre[x] == x)
        return x;
    return findpre(pre[x]);
}

void join(int x, int y)  //加进来
{
    x = findpre(x);
    y = findpre(y);
    if (x == y)
        return;
    else
    {
        pre[y] = x;
        if (r[x] == r[y])
            r[x]++;
    }
}

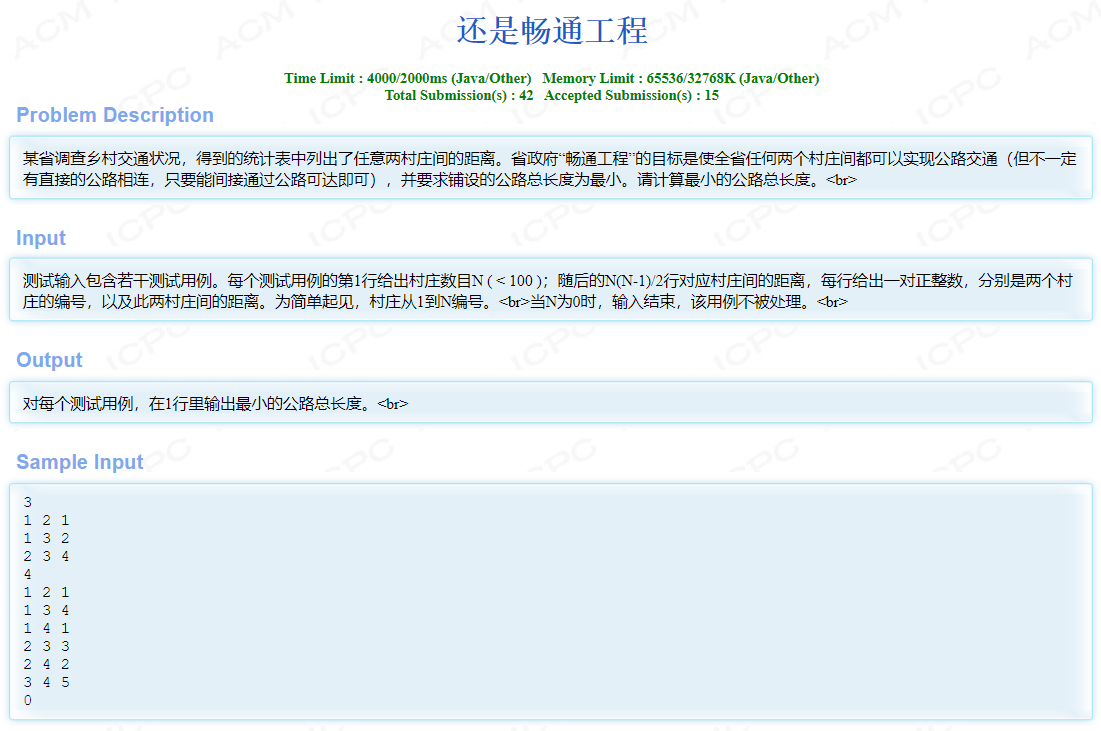
#include <cstdio>
#include <algorithm>
using namespace std;
int f[103];  //村庄的个数，节点
struct ss
{
    int x, y, z;
}a[5000];
bool cmp(ss a, ss b)
{
    return a.z < b.z;
}
int find(int x)
{
    return f[x] == x ? x : find(f[x]);  //查询操作：返回的是x的根结点
}
int main()
{
    int N, n, i, b, c;
    while (scanf("%d", &N), N)
    {
        int s = 0;
        n = N * (N - 1) / 2;
        for (i = 1; i <= N; i++)  //初始化 ，一开始每个村庄都是一个单独的集合，编号从1到n
            f[i] = i;
        for (i = 1; i <= n; i++)
            scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].z);
        sort(a + 1, a + 1 + n, cmp);
        for (i = 1; i <= n; i++)
        {
            int b = find(a[i].x);
            int c = find(a[i].y);
            if (b == c)continue;
            f[c] = b; 	//合并操作
            s += a[i].z;
        }
        printf("%d\n", s);
    }
    return 0;
}