数塔问题

数塔问题

​ 如下图（图片来自百度图片）是一个数塔，从顶部出发在每一个节点可以选择向左或者向右走，一直走到底层，要求找出一条路径，使得路径上的数字之和最大.

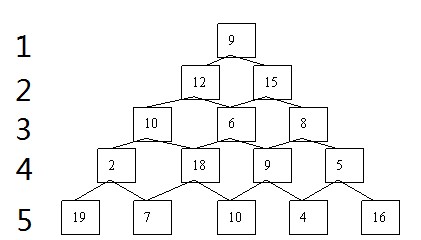
• 在用动态规划考虑数塔问题时可以自顶向下的分析，自底向上的计算。 从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，只要左右两道路径上的最大值求出来了才能作出决策。同样的道理下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。这样一层一层推下去，直到倒数第二层时就非常明了。
• 五层数塔问题可以转化为第五层和两个四层数塔，依次类推下去。

数塔数据存放：data数组

动态规划数据存放：dp数组

一般用数组的方式实现

动态转移方程：

dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + data[i][j]

解释：i为行数，从下往上计算，j为列数。

具体问题：

1. 杭电oj_2084

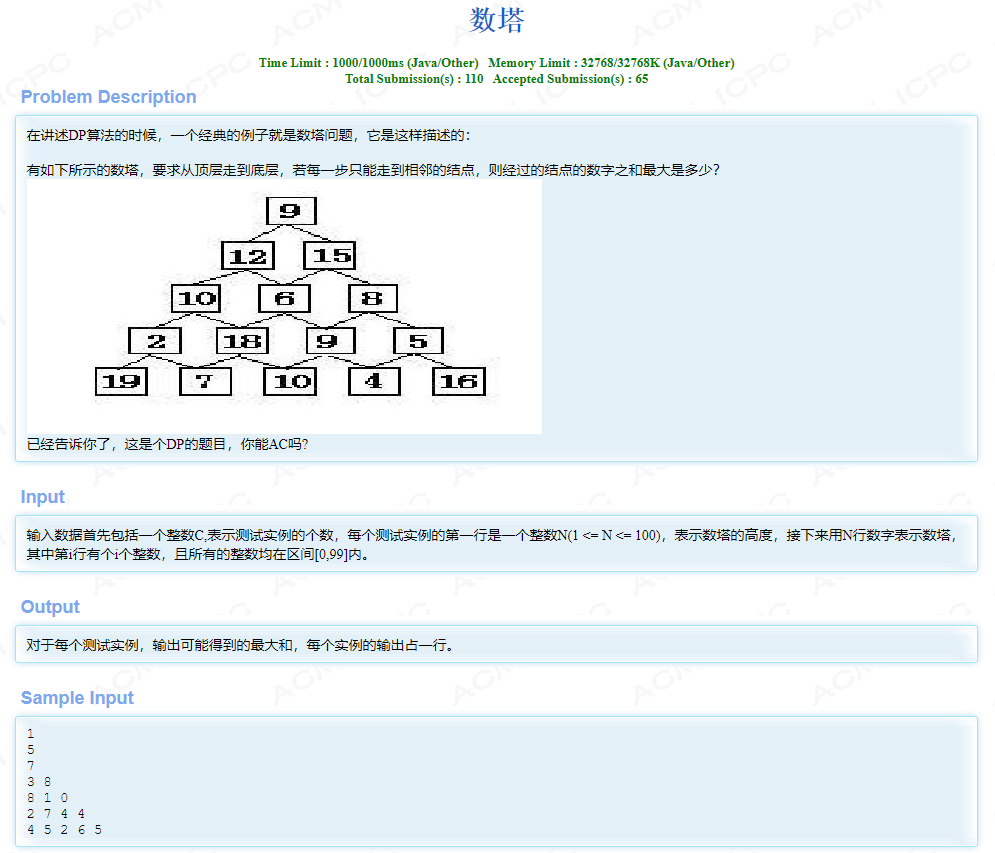
• 样例代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;

int ta[105][105],dp[105][105];//ta存储输入的数据，dp存储状态
int main()
{
    int t;
    while(scanf("%d",&t)==1)
    {
        while(t--)
        {
            memset(ta,0,sizeof(ta));
            memset(dp,0,sizeof(dp));
            int n;
            scanf("%d",&n);
            //输入数据
            for(int i=1;i<=n;i++)
                for(int j=1;j<=i;j++)
                scanf("%d",&ta[i][j]);
                //看清i是逆序
            for(int i=n;i>=1;i--)
                for(int j=1;j<=i;j++)
                dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+ta[i][j];
            printf("%d\n",dp[1][1]);


        }

    }

}

2. 杭电oj_1176

​

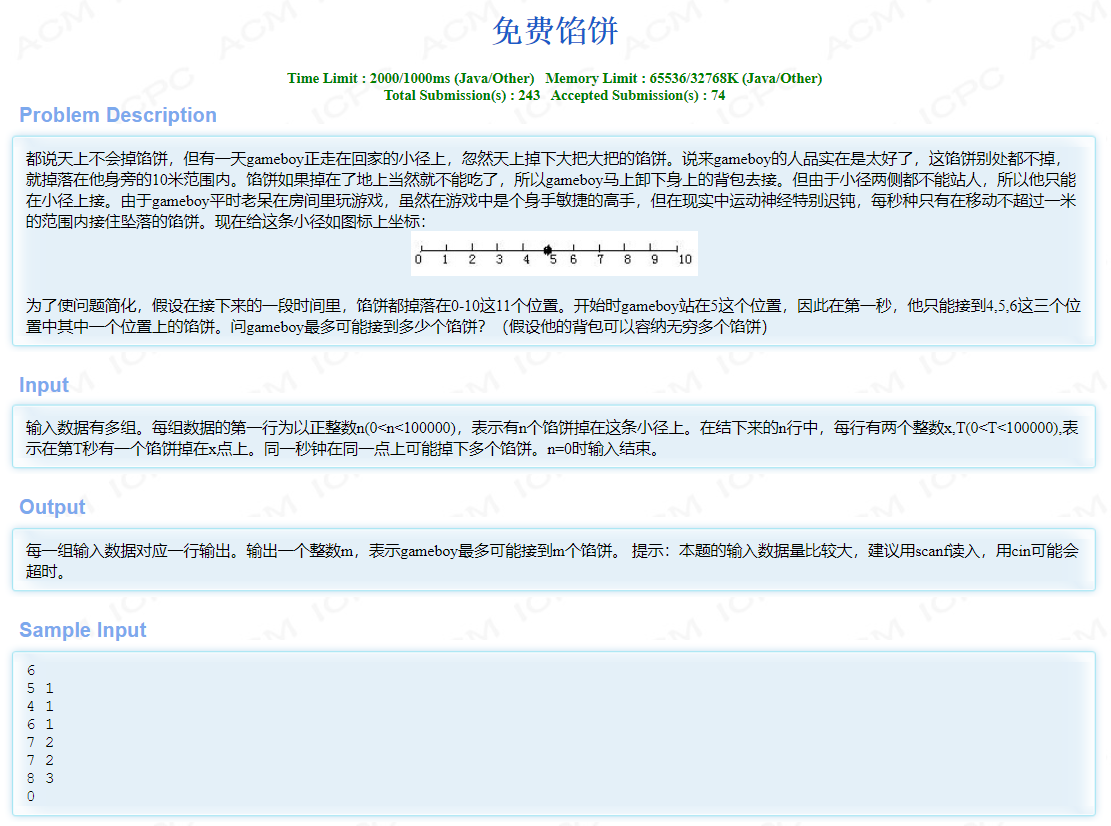
• 问题分析：

  数塔问题的变换形式，时间是原来的层数，位置是原来的列数

  data数组：

  	1	2	3	4	5	6	7	8	9
  3	0	0	0	0	0	0	0	1	0
  2	0	0	0	0	0	0	2	0	0
  1	0	0	0	1	1	1	0	0	0
  0	0	0	0	0	0	0	0	0	0

  bp数组：

  	1	2	3	4	5	6	7	8	9
  3	0	1	1	1	1	3	3	4	0
  2	0	0	1	1	1	1	3	0	0
  1	0	0	0	1	1	1	0	0	0
  0	0	0	0	0	0	0	0	0	0

  动态转移方程为

  DP[T,x]= data[T,x]+ MAX( DP(T-1,x),  DP[T-1,x-1],  DP[T-1,x+1]) 
  

  层数从高到低，秒数也同样从下到上；

  但此题应该注意边缘的计算，因为位置只能从1到9，边缘位置是应该特判。

• 样例代码：

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define  MAX 100005
int a[11][MAX],dp[11][MAX];//a[i][j]第j秒，落在位置i的馅饼的个数
using namespace std;
int max(int,int,int);
int max(int,int);
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        if(n==0)
            break;
        int k=0,p=0;
        memset(dp,0,sizeof(dp));
        memset(a,0,sizeof(a));
        for(int i=0;i<n;i++)
        {
            int x,t;//x表示位置，t表示时间
            scanf("%d%d",&x,&t);
            a[x][t]++;
            if(t>p)//p，记录最后的时间
                p=t;
        }
        for(int j=1;j<=p;j++)
            for(int i=0;i<11;i++)
            {
                if((i+j)<5||(i-j)>5)
                    dp[i][j]=0;
                else if(i!=10&&i!=0)
                    dp[i][j]=a[i][j]+max(dp[i-1][j-1],dp[i][j-1],dp[i+1][j-1]);
                else if(i==10)
                    dp[i][j]=a[i][j]+max(dp[i-1][j-1],dp[i][j-1]);
                else
                    dp[i][j]=a[i][j]+max(dp[i][j-1],dp[i+1][j-1]);
            }
        for(int i=0;i<11;i++)
        {
            if(dp[i][p]>k)
                k=dp[i][p];
        }
        printf("%d\n",k);
    }
    return 0;
}
int max(int a,int b)
{
    return (a>b?a:b);
}
int max(int a,int b,int c)
{
    return _max(_max(b,c),a);
}

3. 杭电oj_1087

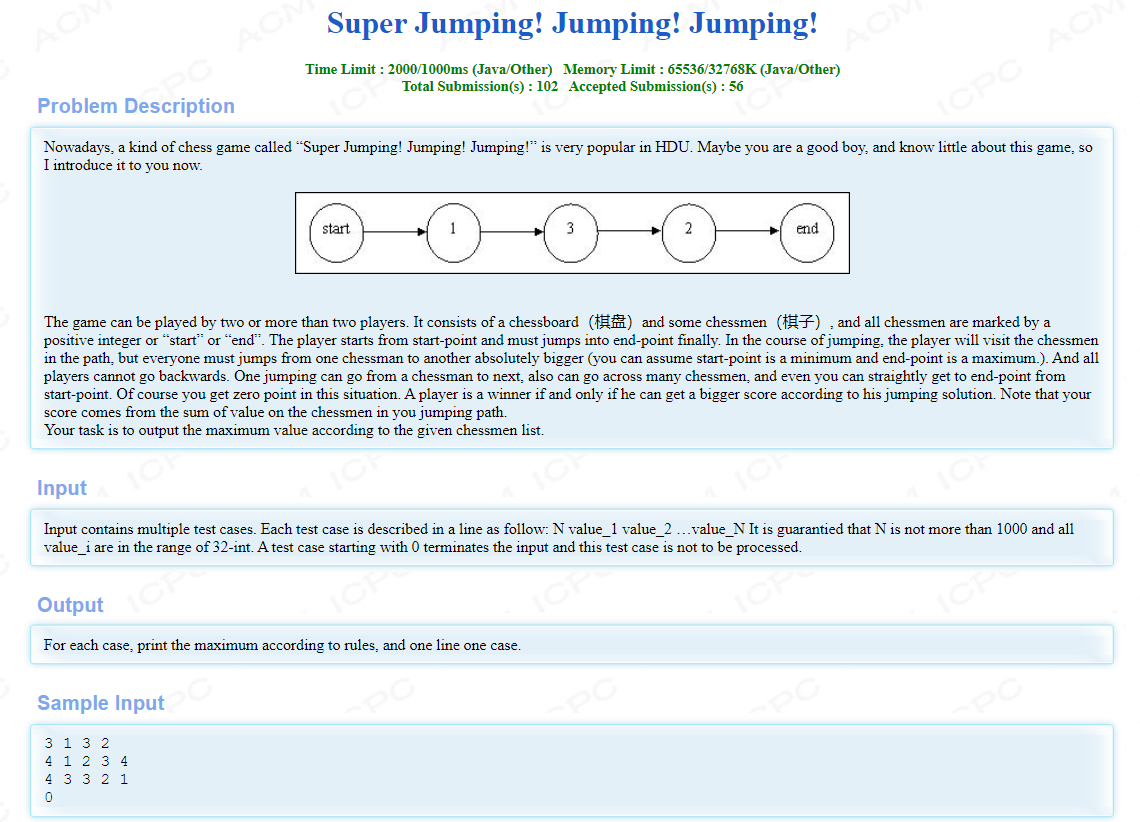
• 问题分析：

  此题状态转移方程为:

  DP[i]=MAX(DP[i],DP[j]+a[i])
  

  其中j<i且a[j]<a[i]

  2	4	j	3	i	6

  DP数组中存放对应到达该位置时的最大步数 计算dp[i]时,从前到i遍历,寻找比a[i]小的元素j,比较a[i]+dp[j]与dp[i],选择大的一个更新为dp[i].

• 样例代码:

#include<iostream>
using namespace std;

long long a[1001], dp[1001];


int main()
{
	int n;
	while (cin >> n)
	{
		if (n == 0)break;
		for (int i = 1; i <= n; i++)
		{
			cin >> a[i];
		}
		long long Max = 0;
		for (int i = 1; i <= n; i++)
		{
			dp[i] = a[i];
			for (int j = 1; j < i; j++)
			{
				if (a[i] > a[j])dp[i] = max(dp[i], dp[j] + a[i]);
			}
			Max = max(Max, dp[i]);
		}
		cout << Max << endl;


	}

}