Dijkstra算法

Dijkstra算法

• 定义介绍 Dijkstra算法是经典的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起点为中心向外层层扩展，直到扩展到终点为止。
• 算法描述 设G=（V，E）是一个带权有向图，初始化一个集合S，表示已经求出最短路径的顶点集合，初始时只有一个源点。按最短路径长度递增的次序依次把除S以外的元素（集合U中元素）加入S中，每次都更新一次各个顶点到源点的距离。直到所有顶点都加入S，最终得到的就是源点到每个顶点的最短路径。
• 具体步骤 以下图为例：
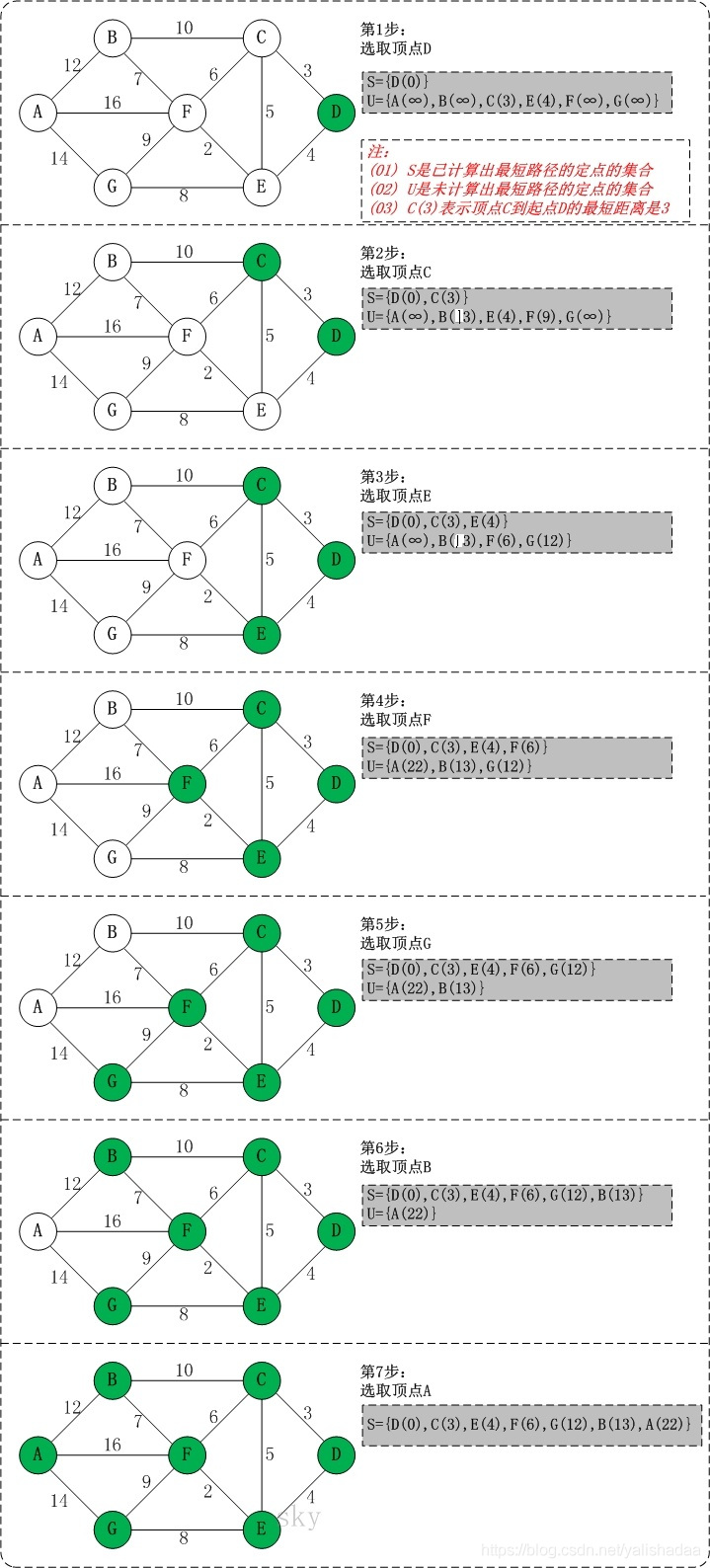
  1. 首先初始化S，将源点D加入，更新所有顶点到D的距离，如果不能直接到达，距离设置为∞。
  2. 选择距离D点最近的顶点C，加入S，其他顶点可以经过C到达D，再次更新到达D的距离。
  3. 重复步骤2，直到所有顶点都加入到S中，S中保存的便是单元最短距离。

//最短路径 - Dijkstra算法 参数：图G、源点v
void Dijkstra(Graph G, int v)
{
	//初始化
	int n = G.vexnum;//n为图的顶点个数
	for (int i = 0; i < n; i++)
	{
		S[i] = false;
		D[i] = G.Edge[v][i];
		if (D[i] < INF)Pr[i] = v; //v与i连接，v为前驱
		else Pr[i] = -1;
	}
	S[v] = true;
	D[v] = 0;
	//初始化结束,求最短路径，并加入S集
	for (int i = 1; i < n; i++)
	{
		int min = INF;
		int temp;
		for (int w = 0; w < n; w++)
			if (!S[w] && D[w] < min) //某点temp未加入s集，且为当前最短路径
			{
				temp = w;
				min = D[w];
			}
		S[temp] = true;
	//更新从源点出发至其余点的最短路径 通过temp
		for (int w = 0; w < n; w++)
			if (!S[w] && D[temp] + G.Edge[temp][w] < D[w])
			{
				D[w] = D[temp] + G.Edge[temp][w];
				Pr[w] = temp;
			}
	}
}

• 全部代码

/*
Project: 图-最短路径-Dijkstra算法
Date:    2019/10/16
Author:  Frank Yu
基本操作函数:
InitGraph(Graph &G)             初始化函数 参数：图G 作用：初始化图的顶点表，邻接矩阵等
InsertNode(Graph &G,VexType v) 插入点函数 参数：图G,顶点v 作用：在图G中插入顶点v,即改变顶点表
InsertEdge(Graph &G,VexType v,VexType w) 插入边函数 参数：图G,某边两端点v和w 作用：在图G两点v,w之间加入边，即改变邻接矩阵
Adjancent(Graph G,VexType v,VexType w) 判断是否存在边(v,w)函数 参数：图G，某边两端点v和w 作用：判断是否存在边(v,w)
BFS(Graph G, int start) 广度遍历函数 参数：图G,开始结点下标start 作用：宽度遍历
DFS(Graph G, int start) 深度遍历函数（递归形式）参数：图G,开始结点下标start 作用：深度遍历
Dijkstra(Graph G, int v)  最短路径 - Dijkstra算法 参数：图G、源点v
功能实现函数：
CreateGraph(Graph &G) 创建图功能实现函数 参数：图G  InsertNode 作用：创建图
BFSTraverse(Graph G)  广度遍历功能实现函数 参数：图G 作用：宽度遍历
DFSTraverse(Graph G)  深度遍历功能实现函数 参数：图G 作用：深度遍历
Shortest_Dijkstra(Graph &G) 调用最短路径-Dijkstra算法 参数：图G、源点v
*/
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<list>
#include<queue>
#include<vector>
#include<map>
#include<iterator>
#include<algorithm>
#include<iostream>
#define MaxVerNum 100 //顶点最大数目值
#define VexType char //顶点数据类型
#define EdgeType int //边数据类型,无向图时邻接矩阵对称，有权值时表示权值，没有时1连0不连
#define INF 0x3f3f3f3f//作为最大值
using namespace std;
//图的数据结构
typedef struct Graph
{
	VexType Vex[MaxVerNum];//顶点表
	EdgeType Edge[MaxVerNum][MaxVerNum];//边表
	int vexnum, arcnum;//顶点数、边数
}Graph;
//迪杰斯特拉算法全局变量
bool S[MaxVerNum]; //顶点集
int D[MaxVerNum];  //到各个顶点的最短路径
int Pr[MaxVerNum]; //记录前驱
//*********************************************基本操作函数*****************************************//
//初始化函数 参数：图G 作用：初始化图的顶点表，邻接矩阵等
void InitGraph(Graph &G)
{
	memset(G.Vex, '#', sizeof(G.Vex));//初始化顶点表
	//初始化边表
	for (int i = 0; i < MaxVerNum; i++)
		for (int j = 0; j < MaxVerNum; j++)
			G.Edge[i][j] = INF;
	G.arcnum = G.vexnum = 0;          //初始化顶点数、边数
}
//插入点函数 参数：图G,顶点v 作用：在图G中插入顶点v,即改变顶点表
bool InsertNode(Graph &G, VexType v)
{
	if (G.vexnum < MaxVerNum)
	{
		G.Vex[G.vexnum++] = v;
		return true;
	}
	return false;
}
//插入边函数 参数：图G,某边两端点v和w 作用：在图G两点v,w之间加入边，即改变邻接矩阵
bool InsertEdge(Graph &G, VexType v, VexType w, int weight)
{
	int p1, p2;//v,w两点下标
	p1 = p2 = -1;//初始化
	for (int i = 0; i<G.vexnum; i++)//寻找顶点下标
	{
		if (G.Vex[i] == v)p1 = i;
		if (G.Vex[i] == w)p2 = i;
	}
	if (-1 != p1&&-1 != p2)//两点均可在图中找到
	{
		G.Edge[p1][p2] = G.Edge[p2][p1] = weight;//无向图邻接矩阵对称
		G.arcnum++;
		return true;
	}
	return false;
}
//判断是否存在边(v,w)函数 参数：图G，某边两端点v和w 作用：判断是否存在边(v,w) 
bool Adjancent(Graph G, VexType v, VexType w)
{
	int p1, p2;//v,w两点下标
	p1 = p2 = -1;//初始化
	for (int i = 0; i<G.vexnum; i++)//寻找顶点下标
	{
		if (G.Vex[i] == v)p1 = i;
		if (G.Vex[i] == w)p2 = i;
	}
	if (-1 != p1&&-1 != p2)//两点均可在图中找到
	{
		if (G.Edge[p1][p2] == 1)//存在边
		{
			return true;
		}
		return false;
	}
	return false;
}
bool visited[MaxVerNum];//访问标记数组，用于遍历时的标记
//广度遍历函数 参数：图G,开始结点下标start 作用：宽度遍历
void BFS(Graph G, int start)
{
	queue<int> Q;//辅助队列
	cout << G.Vex[start];//访问结点
	visited[start] = true;
	Q.push(start);//入队
	while (!Q.empty())//队列非空
	{
		int v = Q.front();//得到队头元素
		Q.pop();//出队
		for (int j = 0; j<G.vexnum; j++)//邻接点
		{
			if (G.Edge[v][j] <INF && !visited[j])//是邻接点且未访问
			{
				cout << "->";
				cout << G.Vex[j];//访问结点
				visited[j] = true;
				Q.push(j);//入队
			}
		}
	}//while
	cout << endl;
}
//深度遍历函数（递归形式）参数：图G,开始结点下标start 作用：深度遍历
void DFS(Graph G, int start)
{
	cout << G.Vex[start];//访问
	visited[start] = true;
	for (int j = 0; j < G.vexnum; j++)
	{
		if (G.Edge[start][j] < INF && !visited[j])//是邻接点且未访问
		{
			cout << "->";
			DFS(G, j);//递归深度遍历
		}
	}
}
//最短路径 - Dijkstra算法 参数：图G、源点v
void Dijkstra(Graph G, int v)
{
	//初始化
	int n = G.vexnum;//n为图的顶点个数
	for (int i = 0; i < n; i++)
	{
		S[i] = false;
		D[i] = G.Edge[v][i];
		if (D[i] < INF)Pr[i] = v; //v与i连接，v为前驱
		else Pr[i] = -1;
	}
	S[v] = true;
	D[v] = 0;
	//初始化结束,求最短路径，并加入S集
	for (int i = 1; i < n; i++)
	{
		int min = INF;
		int temp;
		for (int w = 0; w < n; w++)
			if (!S[w] && D[w] < min) //某点temp未加入s集，且为当前最短路径
			{
				temp = w;
				min = D[w];
			}
		S[temp] = true;
	//更新从源点出发至其余点的最短路径 通过temp
		for (int w = 0; w < n; w++)
			if (!S[w] && D[temp] + G.Edge[temp][w] < D[w])
			{
				D[w] = D[temp] + G.Edge[temp][w];
				Pr[w] = temp;
			}
	}
}
//输出最短路径
void Path(Graph G,int v)
{
	if (Pr[v] == -1)
		return;
	Path(G,Pr[v]);
	cout << G.Vex[Pr[v]]<<"->";
}
//**********************************************功能实现函数*****************************************//
//打印图的顶点表
void PrintVex(Graph G)
{
	for (int i = 0; i < G.vexnum; i++)
	{
		cout << G.Vex[i] << " ";
	}
	cout << endl;
}
//打印图的边矩阵
void PrintEdge(Graph G)
{
	for (int i = 0; i < G.vexnum; i++)
	{
		for (int j = 0; j < G.vexnum; j++)
		{
			if(G.Edge[i][j]==INF)cout << "∞ ";
			else cout << G.Edge[i][j] << " ";
		}
		cout << endl;
	}
}
//创建图功能实现函数 参数：图G  InsertNode 作用：创建图
void CreateGraph(Graph &G)
{
	VexType v, w;
	int vn, an;//顶点数，边数
	cout << "请输入顶点数目:" << endl;
	cin >> vn;
	cout << "请输入边数目:" << endl;
	cin >> an;
	cout << "请输入所有顶点名称:" << endl;
	for (int i = 0; i<vn; i++)
	{
		cin >> v;
		if (InsertNode(G, v)) continue;//插入点
		else {
			cout << "输入错误！" << endl; break;
		}
	}
	cout << "请输入所有边（每行输入边连接的两个顶点及权值）:" << endl;
	for (int j = 0; j<an; j++)
	{
		int weight;
		cin >> v >> w >> weight;
		if (InsertEdge(G, v, w, weight)) continue;//插入边
		else {
			cout << "输入错误！" << endl; break;
		}
	}
	PrintVex(G);
	PrintEdge(G);
}
//广度遍历功能实现函数 参数：图G 作用：宽度遍历
void BFSTraverse(Graph G)
{
	for (int i = 0; i<MaxVerNum; i++)//初始化访问标记数组
	{
		visited[i] = false;
	}
	for (int i = 0; i < G.vexnum; i++)//对每个连通分量进行遍历
	{
		if (!visited[i])BFS(G, i);
	}
}
//深度遍历功能实现函数 参数：图G 作用：深度遍历
void DFSTraverse(Graph G)
{
	for (int i = 0; i<MaxVerNum; i++)//初始化访问标记数组
	{
		visited[i] = false;
	}
	for (int i = 0; i < G.vexnum; i++)//对每个连通分量进行遍历
	{
		if (!visited[i])
		{
			DFS(G, i); cout << endl;
		}
	}
}
//调用最短路径-Dijkstra算法 参数：图G、源点v
void Shortest_Dijkstra(Graph &G)
{
	char vname;
	int v = -1;
	cout << "请输入源点名称:" << endl;
	cin >> vname;
	for (int i = 0; i < G.vexnum; i++)
		if (G.Vex[i] == vname)v = i;
	if (v == -1)
	{
		cout << "没有找到输入点！" << endl;
		return;
	}
	Dijkstra(G, v);
	cout << "目标点" << "\t" << "最短路径值" << "\t" << "最短路径" << endl;
	for (int i = 0; i < G.vexnum; i++)
	{
		if (i != v)
		{
			cout << "  "<<G.Vex[i] << "\t" <<"        "<< D[i] << "\t";
			Path(G,i);
			cout<< G.Vex[i]<< endl;
		}
	}
}
//菜单
void menu()
{
	cout << "************1.创建图       2.广度遍历******************" << endl;
	cout << "************3.深度遍历     4.迪杰斯特拉****************" << endl;
	cout << "************5.退出                     ****************" << endl;
}
//主函数
int main()
{
	int choice = 0;
	Graph G;
	InitGraph(G);
	while (1)
	{
		menu();
		printf("请输入菜单序号：\n");
		scanf("%d", &choice);
		if (5 == choice) break;
		switch (choice)
		{
		case 1:CreateGraph(G); break;
		case 2:BFSTraverse(G); break;
		case 3:DFSTraverse(G); break;
		case 4:Shortest_Dijkstra(G); break;
		default:printf("输入错误！！！\n"); break;
		}
	}
	return 0;
}