Floyd算法

Floyd算法

​ 图使用二维邻接矩阵存储，若无法到达则置为无穷。

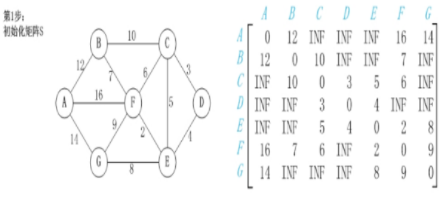
核心代码

void floyd()
{
	for (int k = 1; k <= n; k++)
	{
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				g[i][j] = min(g[i][j],g[i][k] + g[k][j]);
			}
		}
	}
}

最外一层k表示遍历中介点，每个顶点都要作为中介点去运算全局所有顶点

如果

g[i][j]>g[i][k]+g[k][j]

就是说k作为中介点，从i到j通过k比不通过k权值要小，就更新权值。表明有更加合适的路径使权值变小。

比如上图从B到G通过中介A的话会使权值从正无穷变为26

例题

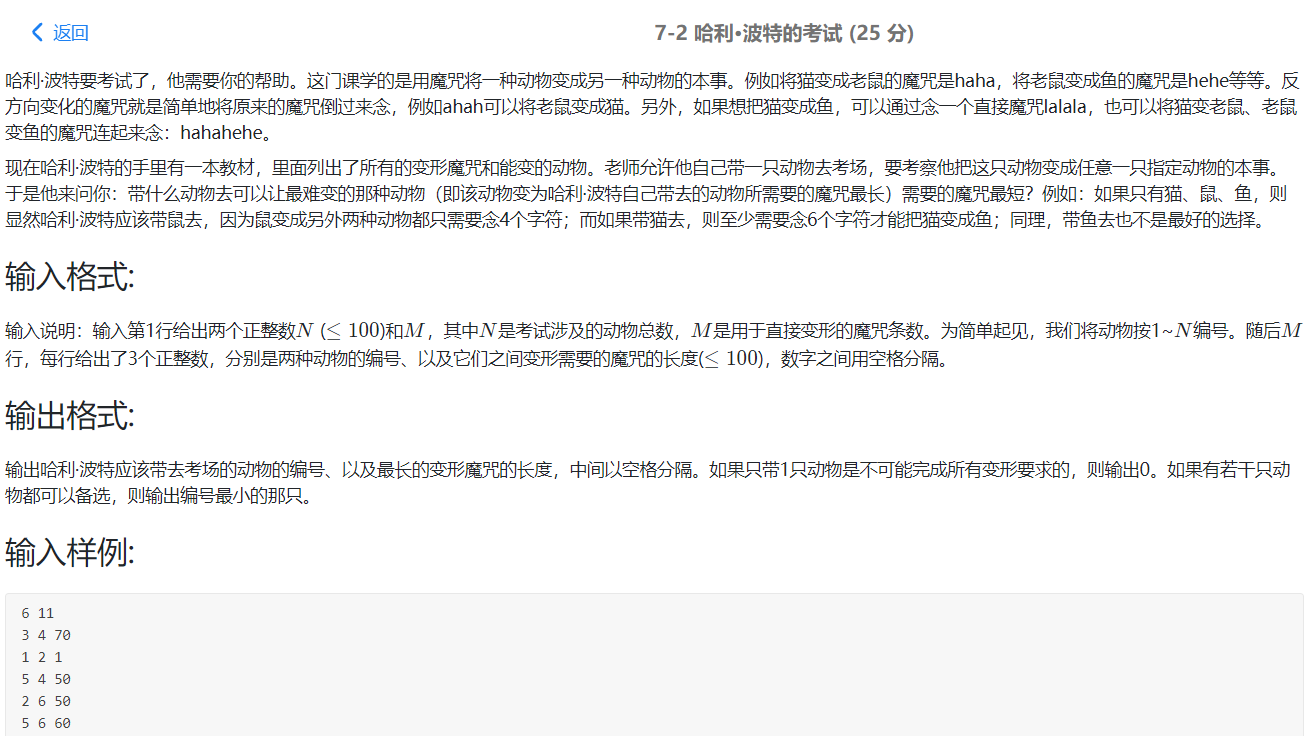
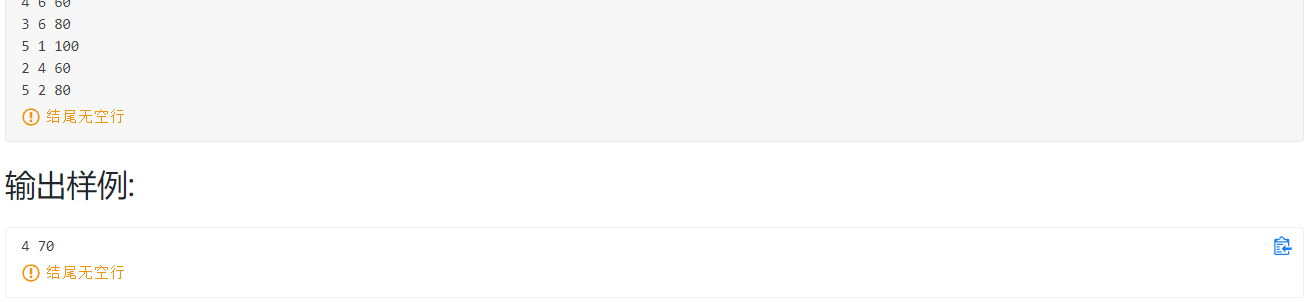
AC代码：

#include<bits/stdc++.h>

using namespace std;

const int maxnum = 110, far = 99999;		//far为默认无穷远
int g[maxnum][maxnum], n, m;

void floyd()
{
	for (int k = 1; k <= n; k++)
	{
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				g[i][j] = min(g[i][j],g[i][k] + g[k][j]);
			}
		}
	}
}

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			if (i != j)
				g[i][j] = far;	//当i=j时，g[i][j]=0
		}
	}

	for (int i = 0; i < m; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;
		g[a][b] = g[b][a] = c;
	}
	floyd();
	int maxdis = far, ansnum = 0;
	for (int i = n; i >= 1; i--)
	{
		int now = 0;		//now代表i节点到最远节点的长度
		for (int j = 1; j <= n; j++)
		{
			now = max(now, g[i][j]);
		}
		if (now <= maxdis)
		{
			maxdis = now;
			ansnum = i;
		}
	}
	if (maxdis == far)
		cout << "0" << endl;
	else
		cout << ansnum << " "<< maxdis << endl;
}